Pythagoras Sats

Häromdagen ringde en släkting till mig och ville ha hjälp med tillämpad matematik. Det var ju lite extra kul eftersom jag gillar det.

Han satt i en grävmaskin och höll på att gräva en rektangulär grop, en husgrund eller något liknande. Han visste att sidorna skulle vara av en viss längd. Men ville ju inte få en skev rektangel. Lösningen är att veta diagonalens längd också - då kan inte rektangeln bli skev. Han ville med andra ord veta ena sidan i en rätvinklig triangel när han kände två av sidorna. Jag illustrerar detta problem i denna bild där jag ger kvadratens sidor namnen a och b, samt ger diagonalen namnet c:

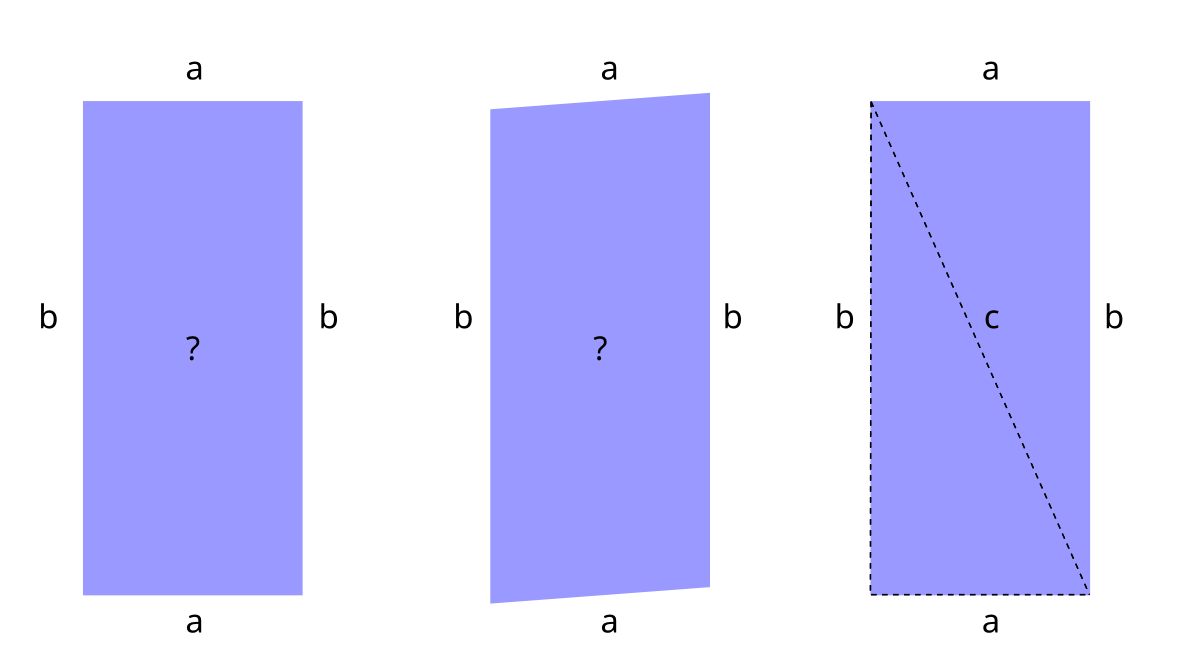
Ni som hängt med i matten i skolan känner igen detta problem som Pythagoras sats. Men det man kanske inte förstått är varför Pythagoras sats gäller. I den här texten tänkte jag förklara vad satsen handlar om och ge ett enkelt geometrisk bevis för den.

Pythagoras sats lyder: för en liksidig triangel är summan av kateternas kvadrater lika med hypotenusans kvadrat (hypotenusan är i vårt fall diagonalen i rektangeln och kateterna rektangelns sidor). Det betyder att a*a + b*b = c*c, om triangeln är liksidig.

Vi börjar med att rita upp gropen som släktingen vill gräva, och en lika stor grop till. Vi lägger dem lite snitsigt inuti en stor kvadrat som får sidan a + b. Som ni ser får vi nu två färgglada kvadrater och våra två rektanglar inuti den stora kvadraten:

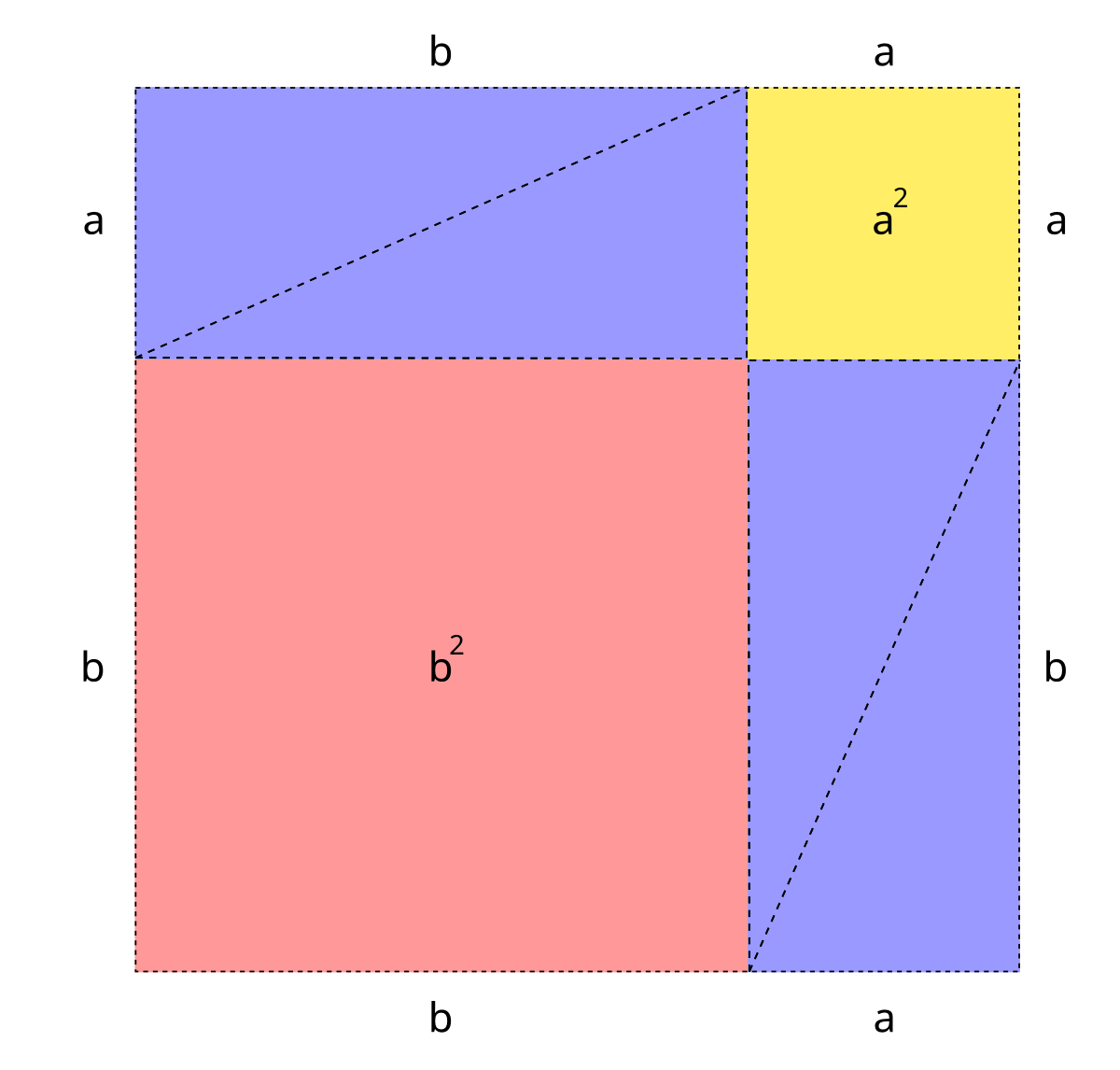
Nu tar vi de två rektanglarna och delar upp dem i fyra trianglar som vi lägger ut i ett annat mönster i samma stora kvadrat. Då får vi en fin grå kvadrat med sidan c i mitten:

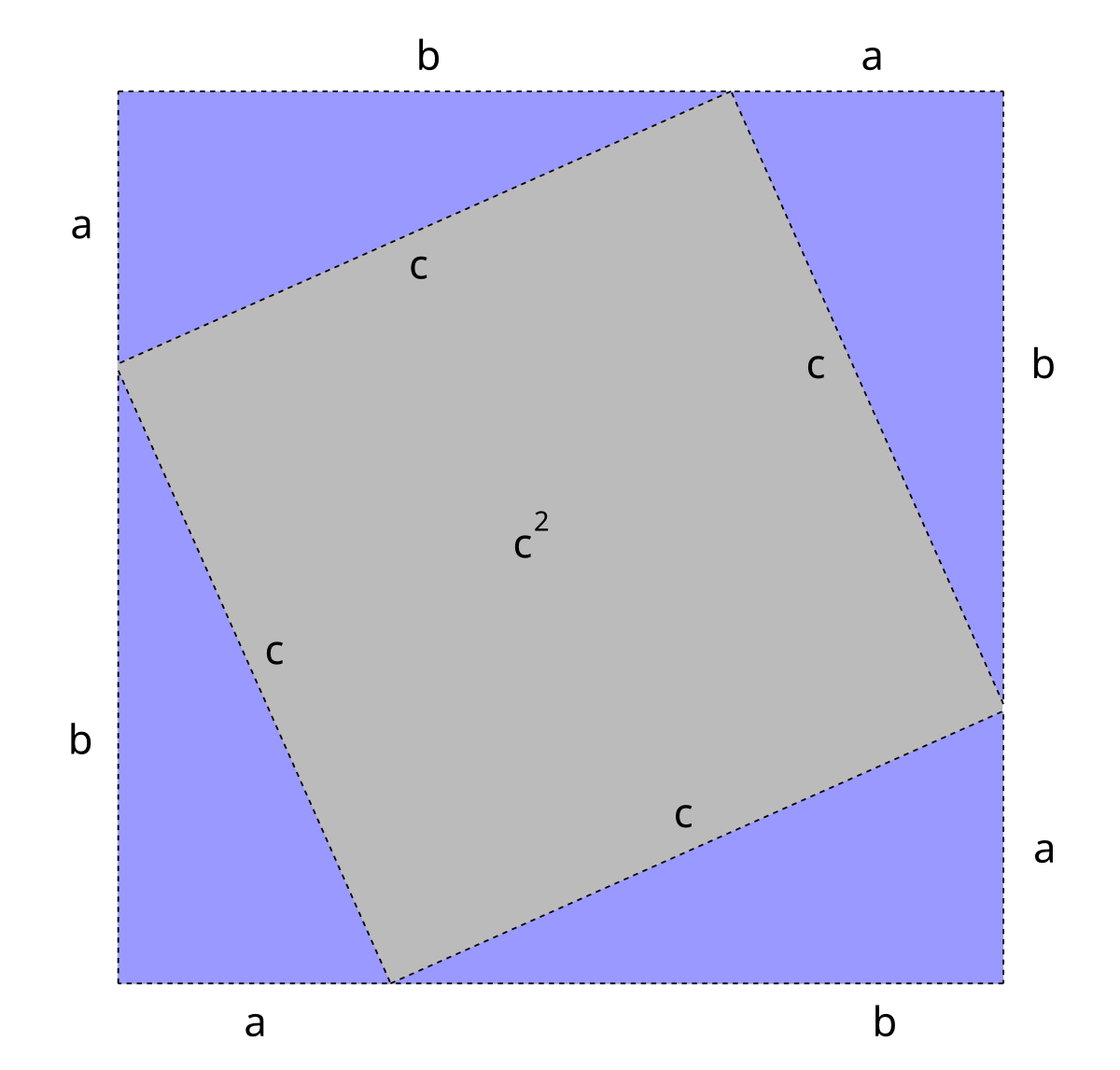
Nu är vi snart klara med vårt bevis. Eftersom den stora kvadraten är lika stor i båda dessa bilder, och våra rektanglar tar lika stor plats i båda bilderna så måste ju de två mindre kvadraternas areal (summan av kateternas kvadrater) vara lika stor som den större kvadratens areal (hypotenusans kvadrat):

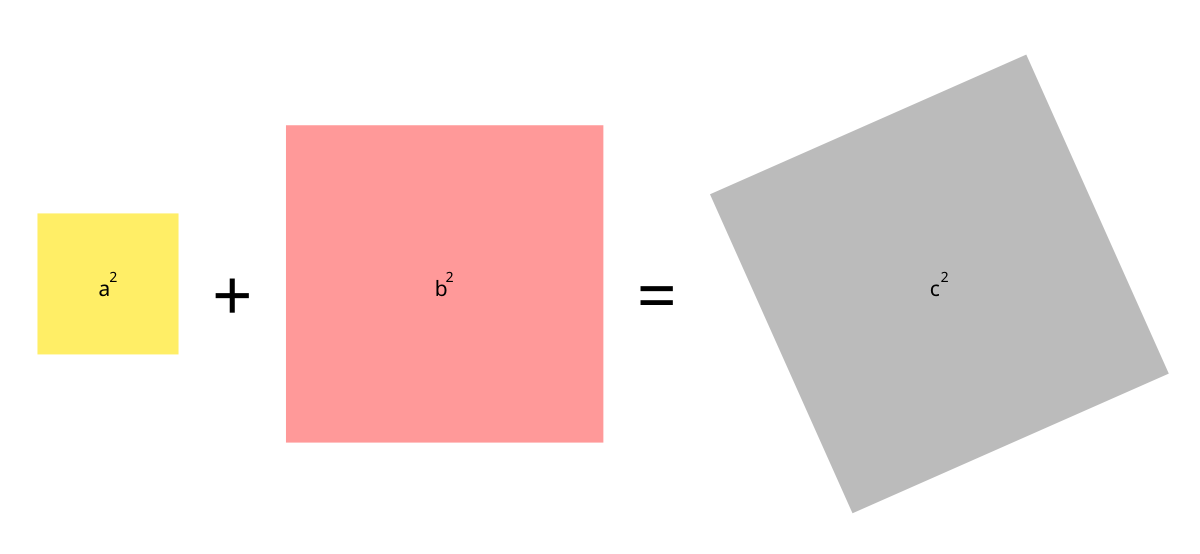
Om vi som exempel hade en rektangulär grop med sidorna 8 meter och 18 meter så blir diagonalen ungefär 19 meter och 69.8 cm (18*18 + 8*8 = 388, och 19.68*19.68 = 388.3024). Bättre noggrannhet än så är nog inte praktiskt genomförbart från hytten i en grävmaskin.

Denna sida tillhör Kategori Plot